189. 旋转数组

Posted on | In
Words count in article: 1.2k | Reading time ≈ 5

题目

给定一个数组，将数组中的元素向右移动 k 个位置，其中 k 是非负数。

示例1：

1
2
3
4
5
6
输入: [1,2,3,4,5,6,7] 和 k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右旋转 1 步: [7,1,2,3,4,5,6]
向右旋转 2 步: [6,7,1,2,3,4,5]
向右旋转 3 步: [5,6,7,1,2,3,4]

示例2：

1
2
3
4
5
输入: [-1,-100,3,99] 和 k = 2
输出: [3,99,-1,-100]
解释: 
向右旋转 1 步: [99,-1,-100,3]
向右旋转 2 步: [3,99,-1,-100]

说明

  • 尽可能想出更多的解决方案，至少有三种不同的方法可以解决这个问题。
  • 要求使用空间复杂度为 O(1) 的 原地 算法。

解答

解法一：

使用额外的数组(不符合题目要求)

Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public void rotate(int[] nums, int k) {
		if (nums.length < 2 || k < 1 || k % nums.length == 0) {
            return;
        }
        
        if (k > nums.length) {
            k = k % nums.length;
        }
        
        int[] newNums = new int[nums.length];
        for (int i = 0;i < k;i++) {
        	newNums[i] = nums[nums.length - k + i];
        }
        
        for (int i = k,j = 0;i < nums.length;i++) {
        	newNums[i] = nums[j++];
        }
        
        for (int i = 0;i < nums.length;i++) {
        	nums[i] = newNums[i];
        }
	}

解法二：

暴力破解

每次旋转一个数字，旋转k个即可。这里有个坑，K的值是有可能比数组的长度大的，所以，在循环处理之前，需要对k取余。

Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public void rotate(int[] nums, int k) {
		int k = k % nums.length;
        for (int i = 0;i < k;i++) {
        	rotate(nums);
        }
    }
	
	private void rotate(int[] nums) {
		int temp = nums[nums.length - 1];
		for (int i = nums.length - 1;i > 0;i--) {
			nums[i] = nums[i - 1];
		}
		nums[0] = temp;
	}

解法三：

翻转数组

假设对数组[1,2,3,4,5,6,7]，需要对k=3进行旋转。

那么我们先把这个数组翻转得到[7,6,5,4,3,2,1].

接着对前k个数字进行翻转，得到[5,6,7,4,3,2,1]

最后，对剩下的数字进行翻转，得到[5,6,7,1,2,3,4]

亦或是

先翻转前length - k 个，得到[4,3,2,1,5,6,7]

在翻转后k个，得到[4,3,2,1,7,6,5]

最后翻转整个数组，得到[5,6,7,1,2,3,4]

Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public void rotate(int[] nums, int k) {
        if (nums.length < 2 || k < 1 || k % nums.length == 0) {
            return;
        }
        
        if (k > nums.length) {
            k = k % nums.length;
        }
        reverse(nums, 0, nums.length - 1 - k);
        reverse(nums, nums.length - k, nums.length -1);
        reverse(nums, 0, nums.length - 1);
        
    }
    
    private void reverse(int[] nums, int start, int end) {
        while (start < end) {
            int temp = nums[start];
            nums[start++] = nums[end];
            nums[end--] = temp;
        }
    }

解法四：

参考的LeetCode官方题解

如果我们直接把每一个数字放到它最后的位置，但这样的后果是遗失原来的元素。因此，我们需要把被替换的数字保存在变量 temptemptemp 里面。然后，我们将被替换数字（temptemptemp）放到它正确的位置，并继续这个过程 nnn 次， nnn 是数组的长度。这是因为我们需要将数组里所有的元素都移动。但是，这种方法可能会有个问题，如果 n%k==0n%k==0n%k==0，其中 k=k%nk=k%nk=k%n （因为如果 kkk 大于 nnn ，移动 kkk 次实际上相当于移动 k%nk%nk%n 次）。这种情况下，我们会发现在没有遍历所有数字的情况下回到出发数字。此时，我们应该从下一个数字开始再重复相同的过程。

现在，我们看看上面方法的证明。假设，数组里我们有 nnn 个元素并且 kkk 是要求移动的次数。更进一步，假设 n%k=0n%k=0n%k=0 。第一轮中，所有移动数字的下标 iii 满足 i%k==0i%k==0i%k==0 。这是因为我们每跳 kkk 步，我们只会到达相距为 kkk 个位置下标的数。每一轮，我们都会移动 nk\frac{n}{k}kn 个元素。下一轮中，我们会移动满足 i%k==1i%k==1i%k==1 的位置的数。这样的轮次会一直持续到我们再次遇到 i%k==0i%k==0i%k==0 的地方为止，此时 i=ki=ki=k 。此时在正确位置上的数字共有 k×nk=nk \times \frac{n}{k}=nk×kn=n 个。因此所有数字都在正确位置上。

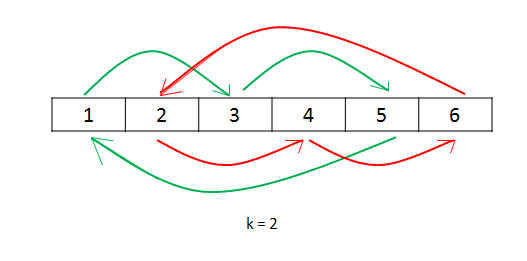
让我们看一下接下来的例子，以更好地说明这个过程：

1
2
nums: [1, 2, 3, 4, 5, 6]
k: 2

Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public class Solution {
    public void rotate(int[] nums, int k) {
        k = k % nums.length;
        int count = 0;
        for (int start = 0; count < nums.length; start++) {
            int current = start;
            int prev = nums[start];
            do {
                int next = (current + k) % nums.length;
                int temp = nums[next];
                nums[next] = prev;
                prev = temp;
                current = next;
                count++;
            } while (start != current);
        }
    }
}
0%